Comecei a estudar Machine Learning há 6 anos na universidade, e há 3 trabalho na área no setor privado. Quando comecei a estudar, nos diversos cursos online e livros que fiz e li, percebi que geralmente são colocados diretamente os métodos, técnicas ou modelos que se usa para “fazer máquinas aprenderem”. Talvez haja alguma introdução sobre estatística, mas nada muito além. Dificilmente se encontra nestas fontes de aprendizado quais são as bases fundamentais do Machine Learning, para que sequer se considere se máquinas podem realmente aprender. Neste texto, pretendo trazer um pouco sobre o cenário mais básico que sustenta a Teoria do Machine Learning.

É claro que qualquer pessoa que gere modelos de machine learning não precisa necessariamente saber desta base. Entretanto, quando se conhece os princípios fundamentais do que se está aplicando, é muito mais fácil e claro ter um pensamento que leve rapidamente a conclusões como do por quê algumas coisas podem ou não funcionar. Uma vez que você conhece a base do machine learning, você pode extrapolar suposições sobre seus dados, seus modelos, etc.

Algumas Definições Importantes

Para construir essa base, primeiro precisamos de algumas definições. Queremos construir a base para “ensinar uma máquina” algum padrão. Este padrão será “aprendido” através de um conjunto específico de dados. Portanto, primeiramente precisamos assumir que existe uma distribuição que gera um conjunto específico de dados, e que esta distribuição é bem definida (i.e., não é ao acaso, mas gera números com certo grau de aleatoriedade). Vamos chamar de $F(x)$ esta função de distribuição desconhecida. Chamamos de $G$ o “gerador de dados” que produz dados vetoriais $x \in \mathbb{R}^n$ i.i.d. (identicamente e independentemente distribuídos) através da função $F(x)$.

Definimos também um supervisor $S$ que é capaz de olhar os dados $x \in \mathbb{R}^n$ produzidos por $G$ e “marcá-los” com um valor $y$. $S$ obedece uma distribuição, também desconhecida, $F(y|x)$. O supervisor é aquele que tem o poder de identificar cada variável $x$ como produtora de um resultado $y$ específico.

Por fim, uma “máquina que aprende” $LM$ (Learning Machine) é capaz de implementar uma função $f(x, \alpha)$, que pega os dados em $x$ e alguns parâmetros $\alpha$, e produz um resultado $\hat{y}$. O objetivo é que o valor-alvo predito $\hat{y}$ se aproxime do valor “real” produzido por $S$, que é $y$.

Para dar um exemplo, imagine que numa certa cidade, o preço de uma casa $y$ é determinado por uma série de fatores: O local da casa, o tamanho, número de andares, número de garagens, idade da casa, etc. Cada uma destas variáveis será um parâmetro $x_i \in x$, e cada $x \in \mathbb{R}^n$ corresponde ao conjunto de fatores de uma certa casa. Estes valores são gerados por um gerador $G$ que obedecem uma função de distribuição desconhecida $F(x)$, e o preço $y$ é determinado por um supervisor $S$ que obedece uma função desconhecida $F(y|x)$. Dado que temos um conjunto de dados gerados por $F(x)$ e $F(y|x)$, podemos modelar o preço de outras casas através de um $LM$ capaz de aplicar a função $f(x, \alpha)$ para obter o “preço estimado” $\hat{y}$ das casas. Se nosso modelo for bom, o preço estimado será muito próximo do preço real $y$. A figura abaixo ilustra este esquema:

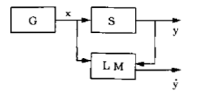
Nosso problema então é: Como fazer nosso $LM$ “aprender” o melhor $f(x, \alpha)$ para aproximar aos resultados de $F(y|x)$, sendo que não conhecemos exatamente esta última função?

Minimizando Riscos

Não temos acesso diretamente às funções que geraram nossas distribuições de dados, porém temos acesso aos dados em si. Então iremos usar os dados em si para estimar o melhor $f(x, \alpha)$. O modo de fazer isso é estimando uma função $f$ qualquer, e então testando o erro (ou “risco”) dessa função. Se conseguimos gerar várias versões de $f$, cada uma com um erro/risco menor que a anterior, eventualmente atingiremos o menor erro possível. Isso é chamado de minimização do risco da função $f(x, \alpha)$.

Podemos definir uma função de custo para calcular o erro $L(y, \hat{y})$, que mede a diferença entre o valor-alvo real e o estimado. Dada esta função de custo, podemos definir também o chamado Risco:

$R(\alpha) = \int L(y, \hat{y}) dF(y|x)$

Mas note que esta integral depende tanto de $L$, a função de custo, quanto de $F(y|x$), a função determinante do valor-alvo que não temos acesso. Como não temos uma função $F(y|x)$ para determinar exatamente o valor de $R$, iremos criar um novo conceito, o de risco empírico. Primeiramente, vamos considerar que nosso conjunto de variáveis e o correspondente valor-alvo real é o par $(x_i, y_i)$ representado por $z_i$, e que existem funções $Q(z, \alpha)$ que recebem nossos pares de dados em $z$ e um conjunto de parâmetros $\alpha$, calcula o valor-alvo estimado $\hat{y}$ e já calcula a função de custo em comparação com o valor-alvo real $y$. Podemos então definir o risco empírico como:

$R_{emp}(\alpha) = \frac{1}{l} \sum_{i=1}^{l} Q (z, \alpha)$

Agora que definimos estes dois tipos de riscos, o real e o empírico, podemos trazer o Princípio ERM: o Princípio da Minimização do Risco Empírico (do inglês Empirical Risk Minimization). Ele é dado como

Para aproximar qual função $Q(z, \alpha)$ minimiza o risco real $R(\alpha)$, precisamos minimizar o risco empírico $R_{emp}(\alpha)$.

Perceba como ambos os riscos dependem dos parâmetros em $\alpha$. Isso significa que o que irá determinar nosso menor risco, e portanto nosso menor erro, e portanto nossa melhor aproximação para a função que calcula $y$ com base nas variáveis em $x$, precisamos escolher os parâmetros certos para nossa função.

Consistência e Convergência do ERM

A partir daqui, a matemática pode ficar um tanto complicada. Vamos pular algumas etapas e algumas provas matemáticas, e nos ater no conceito fundamental para o Princípio ERM: A consistência do processo de aprendizagem de máquina é dado pois o risco real converge ao risco empírico para um conjunto suficientemente grande de dados.

A seguinte imagem ilustra graficamente este conceito:

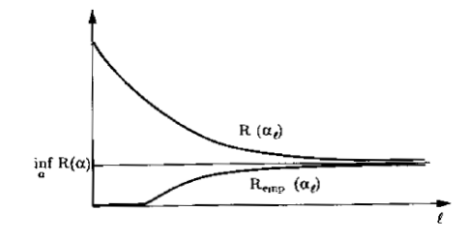
Uma definição matemática interessante para este conceito é que conforme o número de dados ($l$) que você possui cresce, a probabilidade de que o maior valor (supremo) da diferença entre o risco real e o risco empírico ser maior que um valor pequeno $\varepsilon$ tende a ser zero. Escrito matematicamente:

$\lim_{l \to +\infty} P \{ sup (R(\alpha) – R_{emp}(\alpha)) > \varepsilon\} = 0, \forall \varepsilon > 0$

Dizemos então que a convergência será “$\varepsilon$-representativa” baseada na declaração acima.

Conclusão

Definimos não apenas o que é uma máquina que aprende, mas sob que contexto ela aprende: Apenas sob minimização do risco real e convergência com o risco empírico, dado que temos dados suficientes e escolhemos os parâmetros certos em $\alpha$ para que isso aconteça. Essas são algumas das bases fundamentais do Machine Learning.

Perceba que em nenhum momento definimos as funções $F$, $f$, $L$ ou $Q$. Isso se deve por quê o que foi dito acima vale tanto para funções de classificação (que tomam dados $x$ e calculam uma classe para os dados, como $0$ ou $1$), funções de regressão (que calculam $y \in \mathbb{R}$, ou seja, $y$ poderia ser qualquer número real), ou funções de estimação de densidade de probabilidade (que calculam não um valor específico, mas uma função de distribuição para aquele conjunto de dados, como o Estimador de Verossimilhança).

Certamente várias outras coisas precisam ser definidas: Como calcular a melhor função através de um custo? Como escolher uma função de custo? Como saber quando os dados são suficientes para a convergência? Quão rápido o modelo vai convergir? Como posso ter certeza que o modelo vai generalizar bem? Estas perguntas e outras vão ser respondidas ainda neste blog!

Referências

Se gostou do assunto deste texto e quiser saber mais, pode encontrar no livro The Nature of Statistical Learning, por Vladmir Vapnik.