Como algoritmos sabem o que você irá gostar antes de você: Filtragem colaborativa e alternância de quadrados mínimos
Postado originalmente em 14 de dezembro de 2021

Talvez você já tenha parado para pensar sobre como, as vezes, máquinas parecem saber o que você irá gostar antes mesmo que você saiba, ou mesmo pareça que uma máquina está te espionando. Basta você falar de uma coisa que você quer consumir, e essa coisa aparece no seu celular! Parece mágica, mas é apenas matemática. Computadores usam algoritmos de Aprendizado de Máquina para prever o que um usuário possa vir a gostar.
Neste artigo, falarei sobre como aplicativos como Spotify ou Netflix preveem que tipo de músicas ou filmes irão recomendar a você, baseado não só no que você ouve ou assiste, mas também no que pessoas como você estão ouvindo e assistindo. No mundo de Data Science, este tipo de recomendação pode ser feita através de uma técnica chamado Filtragem Colaborativa.
Filtragem Colaborativa
Do inglês Collaborative Filtering, a Filtragem Colaborativa se propõe justamente a realizar previsões automáticas sobre os interesses de alguém, baseado no interesse já conhecido de outras pessoas. Assumimos que duas (ou mais) pessoas parecidas, i.e., que gostam das mesmas coisas, irão continuar gostando das mesmas coisas. Ou seja, se eu e você somos parecidos, e ambos gostamos dos filmes A, B e C, por exemplo, e eu gostei muito do filme D, então é provável que você goste do filme D também.
O modelo não é perfeito e tem algumas limitações. Uma óbvia, por exemplo, é quando eu não sei o que você gosta. Neste caso, não posso comparar seu gosto ao meu, ou de qualquer outra pessoa, para recomendar algo para você. Outro problema comum é um viés de popularidade. Muitas pessoas gostaram do filme Vingadores: Ultimato, logo recomendá-lo para todos pode ser uma alternativa, apesar de que algumas pessoas odeiam filmes de super-heróis, e para elas esta seria uma péssima recomendação. Um terceiro problema típico deste modelo é a escalabilidade. Quanto mais informação eu tiver sobre o gosto das pessoas, mais cálculos vou fazer pra descobrir o que elas podem gostar a mais. Dependendo do algoritmo utilizado, precisarei aumentar meu processamento cada vez mais rápido.
Ainda assim, a Filtragem Colaborativa é extensivamente utilizada para recomendar produtos através de algoritmos. O modelo se popularizou muito após o Prêmio Netflix de 2009, que prometeu $1.000.000 de dólares para o time que melhorasse o algoritmo de recomendação de filmes da Netflix. O time vencedor utilizou um algoritmo chamado Alternating Least Squares (ALS), ou Alternação de Quadrados Mínimos. Abordaremos este algoritmo a partir daqui.
Fatorização de Matrizes
O modelo ALS de sistema de recomendação pode ser matematicamente difícil de ser explicado para não-matemáticos, então vamos usar um exemplo. João, Maria e José assistiram 5 filmes. Cada um deles falou se gostou ou não de cada filme, e o resultado pode ser visto abaixo.
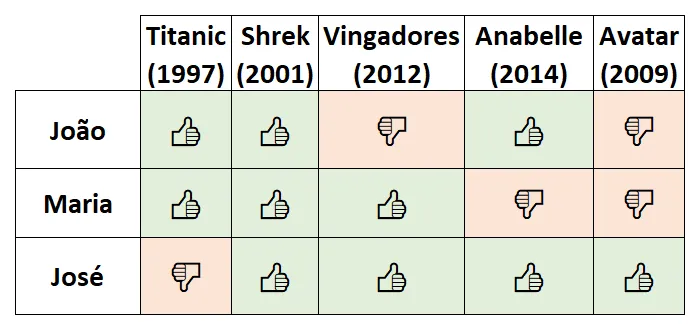
Neste caso, estamos lidando com feedback explícito, pois eles explicitamente marcaram o que gostaram ou não. Caso contrário, teríamos um feedback implícito, que pode ser, por exemplo, quanto tempo uma pessoa assiste um filme antes de dar pausa (isto pode indicar, por exemplo, se ela estava concentrada no filme, mas não garante que seja este o caso), ou simplesmente que filmes a pessoa deu play. O primeiro tipo de feedback é muito mais raro, mas muito mais informativo, afinal a pessoa te disse o que ela gosta. O segundo tipo traz menos informações, afinal a pessoa pode ter assistido o filme inteiro, ou dado play e ter ido fazer outra coisa. Esse segundo tipo, entretanto, é muito mais comum e nos dá mais datapoints para trabalhar.
A tabela acima pode trazer algumas informações. Talvez o João goste de romance, filmes infantis e de terror, mas não de filmes de ação. Já a Maria pode ser adepta de romance, animação e filmes leves com super-heróis, mas não de terror ou filmes de ficção científica. O João pode ser eclético em relação ao que assiste, exceto com filmes de romance, que ele odeia. Tudo isso é inferido da tabela acima, e apenas testes contínuos responderiam se nossa análise está correta.
Agora imagine que o grupo chame mais duas pessoas para assistir filmes: A Ana e o Gabriel. Ana assistiu apenas Vingadores e gostou, enquanto Gabriel gostou de Shrek mas odiou Anabelle.

Como saber se Ana e Gabriel irão gostar dos filmes que não assistiram? O modelo ALS se propõe justamente a preencher os dados não conhecidos através de algo chamado fatores latentes, baseado na fatorização de matrizes.
Vamos “quebrar” a matriz (ou tabela) acima em duas outras matrizes: Uma para as pessoas (usuários) e outro para os filmes (itens). Vamos chamar a matriz original de $R$, e as duas novas matrizes de $P$ e $F$, para pessoas e filmes, respectivamente. A fatorização nos diz que $R$ será aproximadamente igual à multiplicação de $P$ e $F$.
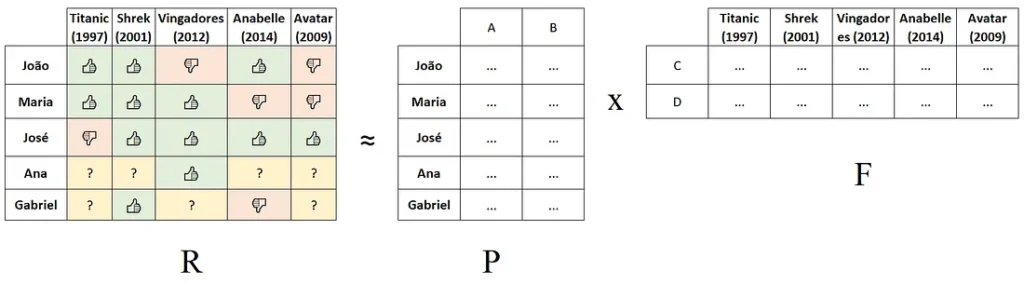
No exemplo acima, as reticências representam os fatores latentes que devem ser preenchidos nas colunas A e B, e nas linhas C e D, para aproximar $P \times F$ de $R$. Se sabemos os dados para João, Maria e José, e alguns dados para Ana e Gabriel, podemos aproximar os fatores latentes para corresponder à informação que já possuímos, e por consequência teremos uma aproximação do resultado total para Ana e Gabriel, incluindo os dados que não existem.
Alternância de Quadrados Mínimos
O modelo ALS tem uma forma de resolver este problema: Iniciamos uma das duas tabelas $P$ ou $F$ com dados aleatórios, e ajustamos a segunda para se adequar à $R$. Digamos que iniciemos $P$ com números aleatórios. Devemos então preencher $F$ com os números que, multiplicando por $P$ (até então aleatório), o resultado será o mais próximo possível de $R$. Com o resultado, calculamos o erro entre nosso $ P \times F $ calculado e $ R $. Voltamos nossa atenção para $ P $: Agora queremos mudar os valores nele para que, novamente, ao multiplicar $P$ e $F$, o resultado seja mais próximo a $R$. Vamos alternando entre as duas tabelas, até que, após algum número de alternâncias, nosso resultado final será muito próximo a $R$, porém com os dados faltantes preenchidos.
A chave aqui é alternar sempre de forma a reduzir o erro entre nossa matriz calculada e a matriz original $R$. O erro nunca será zero, mas tentamos reduzi-lo ao máximo. Este erro é equivalente a
$ argmin_{(P,F)} |R-\tilde{R}| + \alpha |P| + \beta |F| $
onde $R$ é nossa matriz original, $\tilde{R}$ é nossa matriz calculada a partir de $P$ e $F$, e $\alpha$ e $\beta$ são fatores de regularização. O erro pode ser minimizado, por exemplo, com um algoritmo de Gradiente Descendente, que não será abordado neste artigo. Ao final, podemos dizer que, como a equação a seguir mostra,
$ r_{p,f} \approx \sum^n_{j=0} P_{f,j} F_{j,p} $
i.e., o gosto $r$ da pessoa $p$ sobre o filme $f$ será o somatório de $j=0$ até $n$ fatores latentes $j$ do produto escalar entre os vetores latentes do usuário $(P_f,j)$ e do filme $(F_j,p)$. Neste exemplo, escolhemos dois fatores latentes para a matriz de usuários (A, B) e dois para a matriz de filmes (C, D). O número de fatores latentes, porém, deve ser escolhido de forma a otimizar o algoritmo. Quão menor o número de fatores latentes, maior será a abstração do modelo. Um modelo com apenas um fator latente, por exemplo, é equivalente a calcular o filme mais popular e recomendá-lo a todos. Aumentando o número de fatores, aumentamos a personalização, porém caso este fique muito grande, começaremos a recomendar itens para uma pessoa baseado apenas no que ela consumiu (overfitting), e perdemos o poder da filtragem colaborativa.
Além do número de fatores latentes, outros parâmetros podem ser ajustados para este algoritmo, como o número de iterações entre as alternâncias das matrizes, os parâmetros de regularização iniciais, se é possível avaliar um item como negativo, se os dados são explícitos ou implícitos, e neste último caso, a confiança que se dá aos dados fornecidos.
Conclusão
Ao final das contas, caso você receba uma recomendação de um item que você nunca consumiu e que parece que foi feito para você, não é espionagem e nem adivinhação, mas apenas a matemática gerando resultados através de algoritmos computacionais.
Agora, você sabe melhor como estes algoritmos podem se utilizar de dados já existentes para prever gostos que talvez ainda nem existam. Estes algoritmos tem sido extensivamente aprimorados nos últimos anos, e a tendência é que se tornem cada vez mais assertivos. Se hoje podemos descobrir músicas, filmes, jogos, e até itens de supermercado que nunca utilizamos e que descobrimos que podemos gostar, é graças ao trabalho de milhares e milhares de matemáticos, cientistas de dados, entre outros profissionais que tornaram isto possível.